Survey'09_active learning
阅读时间：2023.7.6
作者：Burr Settles，University of Wisconsin–Madison
来源：
日期：2009
有无代码:无
0.摘要：
- 定义：主动学习的关键是使用，我们能够挑选信息度较高的训练数据，使得训练出来的算法能比在所有数据上标注训练达到更高的性能。
- 论文内容包括
- 介绍
- 方案
- 查询策略框架
- 关于主动学习的实证分析和理论分析
- 问题设置变体
- 实际问题考虑
- 相关研究领域
1.引言
1.1主动学习是什么
- 首先算法允许选择特定的有标签的训练数据
- 关键假设：标注是有成本的。
- 语音识别
- 信息提取
- 分类和过滤
- 目标：使用尽可能少的标记数据来训练解决问题的模型，提高精度。
1.2 例子
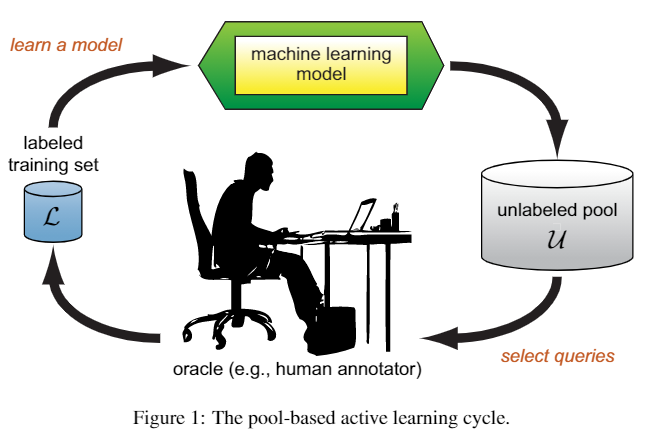图1 基于池的主动学习循环
从标记样本集$\mathcal{L}$中的少量样本出发，生成对未标记样本池中的特定样本请求（人类注释者）标签，并从标记结果进行学习。
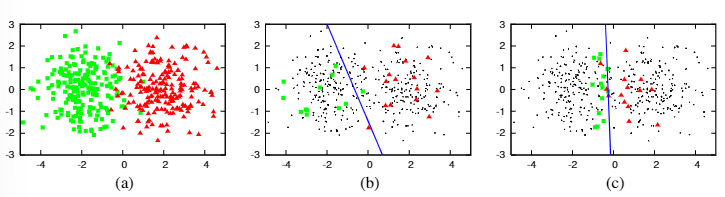图2 阐释性例子
（a）是由两个高斯函数生成的数据集，不同的颜色代表不同的类 （b）随机采样三十个点，标注后训练逻辑回归模型，分类精确度达到70%。分类边界是倾斜的，远离最佳决策边界x=0的位置。 （c）使用不确定性采样来关注最接近决策边界的实例，使得模型空间充分解释其他部分的实例，避免为冗余或者不相关的实例请求标签，在30个实例被标记的情况下达到90%的准确率。
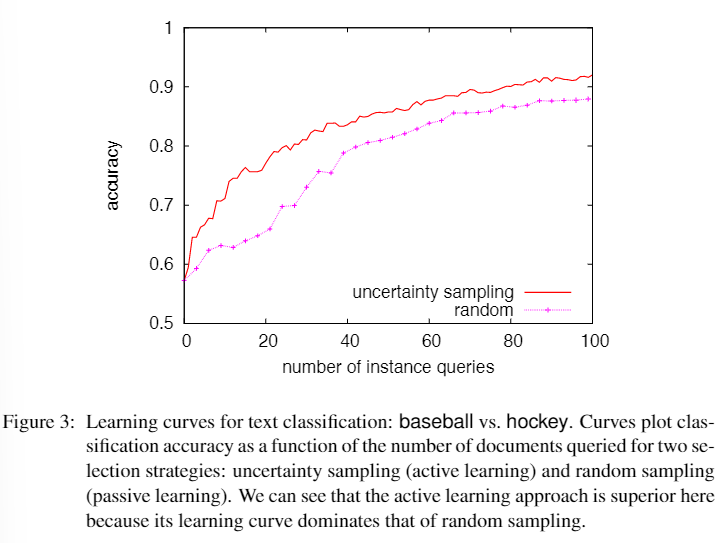图3 在图分类任务上（主动学习的）模型准确度在大部分点上都由于随机采样训练的模型
2. 查询生成方案
假设：查询的形式是某些未标记的实例，经过查询后，他们会被oracle预言机标记。
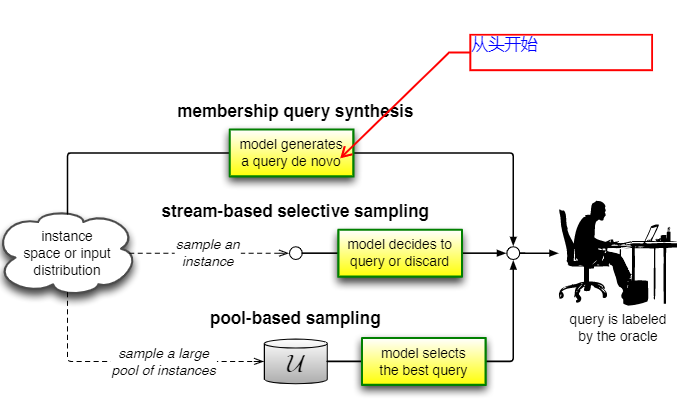
2.1 Membership Query Synthesis（成员查询综合）
- learner可以请求任何未标记实例的标签,一般择最有信息量的样本进行标注。图像从头开始生成新的查询。
- 缺点：在训练神经网络对手写字符进行分类时，发现学习器生成的许多查询图像不包含任何人类可识别的符号。同样可以想象到在自然语言处理任务上同样会出现无语义的查询。后续两节中基于流和基于池的方案可以解决这种限制。
2.2 Stream-Based Selective Sampling（基于流的选择性采样）
假设：获取未标记样本除标签之外的信息是免费的、或者远远小于请求标注的成本，因此可以首先在建模未标记样本的空间，在未标记样本集$\mathcal{U}$中采样，让学习器来决定是否请求它的标签。
这里有多种方式来决定是否查询该未标记样本。
- 一种常用的方法是使用不确定性度量，例如熵（entropy）或置信度（confidence），来衡量模型对于该采样样本的不确定性，使得信息量越大的实例越有可能被查询。
- 另一种方法是计算实例空间中对学习者仍然不明确的部分，只查询落在其中的未标记样本。或者设定一个信息量的最小阈值，只查询高于此阈值的实例。
- 另一种更有原则的方法是定义整个模型类仍然未知的区域，即与当前标记训练集一致的假设集，称为版本空间。如果同一模型类（但参数设置不同）的任何两个模型在所有标记数据上都一致，但在某些未标记实例上不一致，则该实例位于不确定性区域内。
2.3 Pool-Based Sampling（基于池的采样）
假设：有一小部分标记数据$\mathcal{L}$和大量可用的未标记数据 $\mathcal{U}$。有选择地从池中选择查询，通常，根据用于评估池中所有实例的信息性度量，以贪婪（最优）的方式查询实例。
- stream-based 和pool-based的区别在于前者是按顺序扫描样本，由learner做出是否查询的决策，就这在选择查询之前对整个集合进行评估和排名。
- 虽然基于池的策略在论文发表中更常见，但是基于流的策略在内存或计算能力有限时，适应地更好。
QAL很有可能采用这种方案，通过量子计算的数学框架对样本空间进行建模，定义合适的不确定性度量。
3. 查询策略框架
假设：查询选择算法$A$和信息量最丰富的实例（最佳查询）$x_{A}^{*}$
3.1 Uncertainty Sampling
这里给出三种不确定性度量算法，用于选择查询样本。
第一种是查询最不可信的实例样本，选择被预测的最有可能类的概率的最小值的样本进行查询，或者最大化不是最有可能类的概率的样本进行查询。公式如下：
\[x_{LC}^{*}=\underset{x}{\mathrm{argmax}}\ 1-P_{\theta}(\hat{y}|x)\]其中 $\hat{y}=\mathrm{argmax}{y}{P{\theta}({y}\mid x)}$
然而上述方法只考虑了最有可能的标签，丢弃了有关剩余标签的信息。为了纠正这种问题，出现了多类不确定性采样的变体，叫margin sampling（边际采样）。
\[x_{M}^{*}=\underset{x}{\mathrm{argmin}}\ P_{\theta}(\hat{y_1}|x)- P_{\theta}(\hat{y_2}|x)\]其中$\hat{y}_1$和$\hat{y}_2$分别是模型下最有可能和第二有可能的标签。因为分类器毫无疑问区分两个最可能的类标签。边缘较小的实例更加模糊，因此了解真实标签将有助于模型更有效地区分它们。但是对于标签类别较多，该方法仍然忽略了剩余类的大部分分布。
于是出现了更加通用与流行的策略：用熵进行度量。
\[x_{H}^{*}=\underset{x}{\mathrm{argmax}}-\sum_{i}P_{\theta}(y_{i}|x)\log P_{\theta}(y_{i}|x)\]$y_i$涵盖所有可能的标签类别。熵是一种信息论度量，表示“编码”分布所需的信息量。
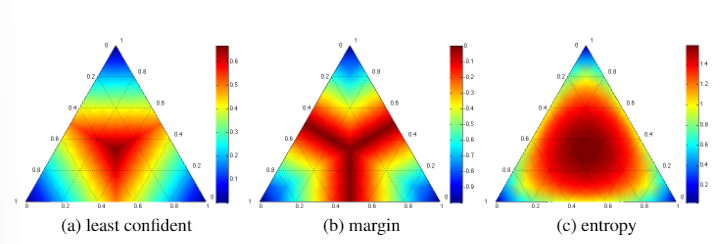图5 在三分类任务中的热力图。单纯形角表示一个标签具有非常高概率的位置。每个信息最丰富的查询区域以深红色显示，从中心向外辐射。
直观上来说，如果目标函数是最小化对数损失，那么熵似乎是合适的，而如果我们的目标是减少分类误差，那么其他两个（特别是边际）更合适。
在高斯假设下，随机变量的熵是其方差的单调函数，因此这种方法与用于分类的基于熵的不确定性采样的精神非常相似。可以针对各种模型计算输出方差的闭合形式近似值，包括高斯随机场（Cressie，1991）和神经网络（MacKay，1992）。回归问题的主动学习在统计文献中有着悠久的历史，通常被称为最优实验设计（Federov，1972）。这些方法避免了不确定性采样，而是采用更复杂的策略。
3.5 Variance Reduction
4. 关于主动学习的实证分析和理论分析
5. 问题设置变体
6. 实际问题考虑
7. 相关研究领域
This line appears after every note.